Outline

8. Numerical Solutions

We assume independent variables 0 < m < M and t,
and dependent variables r, ρ, T, l, and X (the vector of nuclear composition, which will evolve as the star ages).
The "four" equations for stellar structure assuming quiescent aging are:

4πr ²ρdr = dm
central boundary condition: r = 0 at m = 0.

dl = ε dm
central boundary condition: l = 0 at m = 0.
Gravitational and Nuclear energy generation: ε = ε (ρ, T, X ) ergs/gram.

dP = −Gmρ dr /r ² or
4πr ⁴dP = −Gm dm
surface boundary condition: P = 0 at m = M.
Equation of State: P = P (ρ, T, X ).

Radiative layers
64π ²r ⁴ac T ³dT = − 3κ l dm
surface boundary condition: T = 0 at m = M.
Mean opacity: κ = κ (ρ, T, X ) cm²/gram.

Convective layers
P dT = T(1−1/γ) dP
surface boundary condition: set by radiative boundaries.
And r, P, T, and l continuous across convective-radiative interfaces.
(Note: ρ and X need not be continuous, although denser layers cannot reside above less dense layers.)
Adiabatic constant: γ = γ (ρ, T, X )

The four equations and the continuity requirements across interfaces suggest that P might be a better dependent variable than ρ, but we are so used to writing the coefficients as functions of ρ and T that I have chosen ρ for the tracked variable. If the equation of state has the form P = P_o (ρ/ρ_o) ^β (T/T_o) ^α, then dP/P = β dρ/ρ + α dT/T.

Polytropes
If we can write the equation of state as P = P_o (ρ/ρ_o) ^1+1/n, then the first two equations form a complete set, and we can solve them independently from the temperature structure. Such a system is said to be a polytrope of index n. Often polytropes are good approximations to real stars, and make good initial models for the iterative schemes described below.

Numerical Solutions
Computationally one calculates values of the dependent variables on a predetermined (or adaptive) grid of m-values. We choose m rather than r for the grid since we know the total mass M but not the radius R. Ideally, we will want to choose combinations of variables and/or particular schemes of gridding to make the problem more linear and account for wide variations of pressure and density and rapid changes near the surface. Refer to the literature if you are so inclined. As an example, lets replace m with (M − ζ) /M, and write the equations in terms of logarithmic variables. Then all combinations of terms are dimensionless fractions, and equal steps in ln (ζ ) favor the surface where state variables change rapidly.

Define y_m as the vector of dependent variables (ln r_m, ln l_m, ln ρ_m, ln T_m) at grid point m (assume the X_m are part of the coefficient functions). The elements of y_m are y_j,m, 1 ≤ j ≤ 4. Then we may write all four equations as the vector equation

Ι · dy = f ( y) d lnζ

e.g.

x1x	0	0	0		d ln r		− ζ M /4πr 3ρ
0	x1x	0	0		d ln l		− ζ M ε /l
0	0	xβx	xαx	x•x	d ln ρ	x=x	ζ MGm/4πr 4P	d lnζ
0	0	0	1		d ln T		3ζ Mκ l /64π 2r 4acT 4
0	0	− β∇ad	1 − α∇ad				0

Terms in the continuity equation have been highlighted for example.
Note that the matrix Ι is nearly the identity matrix (empty except ones on the diagonal; it would be the identity matrix if we choose P as a dependent variable and have no convection). It is independent of state variables although α and β are depth-dependent and will vary slightly from iteration to iteration.
We may replace each differential equation with a difference equation:

Ι · dy = f ( y) d lnζ xx → xx Ι_m+1/2 · (y_m+1 − y_m) = f_m+1/2 Δlnζ,

where the subscript m+1/2 indicates the value of the function halfway between m and m+1, usually taken as the average of the values at m and m+1.

The transcontinental railroad method (my nomenclature)
When these equations were first solved numerically either by hand or on mechanical desk calculators, the prefered process was to assume values of the unknown variables at the two boundaries, and integrate outward from the center and inward from the surface with the intention of matching the solutions at some mid-point. Let's say that the matching errors at any one iteration i are Δr_i, Δl_i, ΔP_i, and ΔT_i. The idea is to adjust the four unknown boundary values until all four mid-point variables are continuous.

Make small changes in each boundary value T_c, ρ_c, l_s, r_s, one at a time, and deduce the 16 partial derivatives ∂Δr_i /∂T_c, etc.
Then solve the four equations in four unknowns

(∂Δr_i /∂T_c) δT_c + (∂Δr_i /∂ρ_c) δρ_c + (∂Δr_i /∂l_s) δl_s + (∂Δr_i /∂r_s) δT_s = −Δr_i ,
etc.

for the corrections δT_c, etc. to apply to the boundary values in order to get a better solution. Iterate as needed. How many grad students on how many calculators will it take to solve this problem in a finite time?

Newton-Raphson iteration
With fast and accurate computers, the prefered method now (which allows for obscure and difficult contributions to the transfer coefficients) is Newton-Raphson iteration. Interiors astronomers call it the Henyey method after Louis Henyey, the first to apply it to structural problems. Atmospheres astronomers call it complete linearization, using a term popularized by Dimitri Mihalas. The idea is to start with some guestimate solution (e.g. a polytrope or a model for a similar star) and calculate corrections throughout the model that bring one closer to a true solution.

Begin by replacing every variable y_j;m with (y_j;m + δy_j;m), where in this new form y_j;m is the present iteration value and δy_j;m is the correction required to reach the true solution. Also write the vector elements f_j;m as the first order expansion f_j;m [1 + ∑ _k (∂ln f_j;m /∂y_k) δy_k;m]. As an example, the f-element ( − ζ M ε /l ) becomes

f_2;m x → x (− ζ_m M ε_m /l_m ) (1 + λ δlnρ_m + ν δlnT_m − δlnl_m )

where λ and ν are the power exponents for ρ and T, respectively, of the energy generation ε (now one sees why we use power laws). Equation j may now be written

∑ _k Ι_j,k;m+1/2 (y_k;m+1 + δy_k;m+1 − y_k;m − δy_k;m) =
0.5 { f_j;m+1 [1 + ∑ _k (∂ln f_j;m+1 /∂y_k) δy_k;m+1] + f_j;m [1 + ∑ _k (∂ln f_j;m /∂y_k) δy_k;m]} Δlnζ

Collect all δy terms on the left and all known terms on the right, and express in vector form:

Ι_m+1/2 · (δy_m+1 − δy_m) − 0.5 (F_m+1 · δy_m+1 + F_m · δy_m) Δlnζ = f_m+1/2 Δlnζ − Ι_m+1/2 · (y_m+1 − y_m) .

Here the matrices F_m contain the 16 f_j;m ∂ln f_j;m /∂y_k values. Notice that the right-hand side consists of the inhomogeneous error source terms, and reduces to zero (one hopes) at iteration convergence. The left-hand side consists of only linear terms containing the desired corrections δy_m.

We have one such vector equation for each depth point. In total, there are 4×M linear equations in that many unknowns, where M is the number of depths. With today's computers, it is not dificult to do a direct inversion of a 1000×1000 matrix, so we could solve this set by brute force for a model containing up to 200-300 depths. However, in so doing we would be accomplishing a large number of multiplications of zero times zero. We can be much more elegant, doing only those calculations which are necessary.

First, split the vector equation into two parts depending on the location of the boundary conditions. For j = 1,2, write the difference equation for depth m over m and m+1 as above. At depth m = M, replace the difference equation with the boundary conditions δln r_M = 0 and δln l_M = 0, since we already know the values of r and l here. (Note that ln(0) is a pretty big negative number; one will need to end the model just short of the center and assume negligible but non-zero values for r and l.) For j = 3,4, write the difference equation for depth m over m and m−1. At depth m = 1, replace the difference equation with the boundary conditions δln ρ₁ = 0 and δln T₁ = 0, since we already know the values of ρ and T here. (With similar caveats on logarithmic values.) Then the "brute force matrix" of variable coefficients that we need to invert looks like:
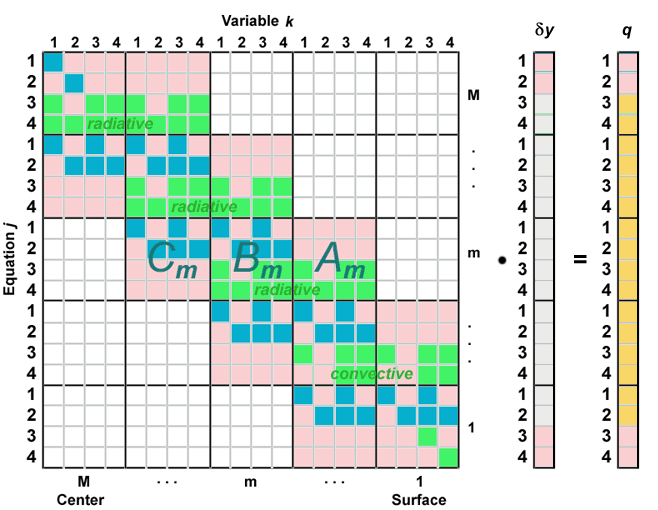Non-zero elements are blue (equations j = 1,2) and green (equations j = 3,4). The pink elements are zero, but fill out elements still necessary for the computation. This kind of matrix is called block tri-diagonal, and many mathematics packages have routines for inverting such matrices. It pictures a series of linear equations that may be written

− A_m · δy_m−1 + B_m · δy_m − C_m · δy_m+1 = q_m ,

where A_m, B_m, and C_m are 4×4 matrices and q_m is the 4-vector of errors at depth m.

Assume a recursion relation

δy_m−1 = D_m · δy_m + p_m

and substitute into the ABCq equation:

− A_m · (D_m · δy_m + p_m) + B_m · δy_m − C_m · δy_m+1 = q_m .

Now solve for δy_m:

δy_m = (B_m − A_m · D_m)⁻¹ (C_m · δy_m+1 + A_m · p_m + q_m).

By comparison with the recursion relation above, we may write:

D_m+1 = (B_m − A_m · D_m)⁻¹ C_m,
p_m+1 = (B_m − A_m · D_m)⁻¹ (q_m + A_m · p_m).

The numerical solution then proceeds thusly: starting at m = 1 (where A_m = 0) begin sequentially storing the recursion coefficients D_m+1 and p_m+1 (we will not need D₁ and p₁). At m = M, the ABCq equation looks like the recursion relation:

− A_M · δy_M−1 + B_M · δy_M = q_M
− A_M · δy_M−1 + A_M · D_M · δy_M = − A_M · p_M .

Subtract these two equations and solve for δy_M:

δy_M = (B_M − A_M · D_M)⁻¹ (q_M + A_M · p_M)

Now we may back-substitute through the recursion relation using the stored coefficients, and we are done. Iterate as necessary.

While the Henyey method may seem much more computationally intensive than the transcontinental railroad method (and it is), it is much more robust. There are situations where very small changes in the 'unknown' boundary values result in very large (even infinite) fluctuations at some pre-determined matching boundary. Also, the TCR method does not handle discontinuities in X and ρ very well, since it doesn't 'know' what to expect on the other side. Radiative-convective boundaries present a similar though less severe problem. In the Henyey method, each grid-point is 'aware' of all the other grid points through the accumulation of the recursion coefficients.

Time integration
As long as dynamic terms are small, we may assume a sequence of hydrostatic models. The lagrangian acceleration d ²r/dt ² = − 4π r ²∂P/∂m − g. At some point in the aging process no sequential hydrostatic model will satisfy the relation d ²r/dt ² << g for all levels. An equivalent check is dr/dt << v_sound. Pulsation may be setting in, high luminosity may be driving rapid mass loss, the core may be initiating catastophic collapse, etc. Prior to that point, hydrostatic aging still implicitly involves time through the evolution of X, and may explicitly involve time through the expansion/contraction term in the luminosity equation.

For nuclear evolution, one only need advance the aging with time steps that match the changing concentrations of interest. The forward integration usually may proceed explicitly; that is, future times may be calculated from present and recent past times. For example,
X_j,n = X_j,n−1 + Δt dX_j /dt |_n−1 + 0.5 Δt (dX_j /dt |_n−1 − dX_j /dt |_n−2).

Nuclear evolution is accompanied by structural change, through the change in mean molecular weight/particle number.

Implicit formulae
Implicit time integration makes use of data at the time step being calculated, and is more robust than explicit integration for the same reason that Newton-Raphson methods are more robust than the TCR method. Consider the energy equation with the expansion/contraction term:

dl = (ε_nuc + ε_grav) dm = [ε_nuc − P (d lnP/dt − Γ₁ d lnρ/dt) /ρ (Γ₃ − 1)] dm .

Expressing the time terms in difference form (we will leave it to the reader to follow through with the space differencing)

dl_n = {ε_nuc;n − P_n [(lnP_n − lnP_n−1) /Δt − Γ_1;n (lnρ_n − lnρ_n−1) /Δt] /ρ_n (Γ_3;n − 1)} dm .

Terms on the right hand side are all understood functions of our state variables at time iteration n, except for some added known information from n−1.

Notice that iteration n−1 data enters only through the explicit time difference quantities lnP_n−1 and lnρ_n−1 (and the values of X_j,n necessary to determine ε_nuc;n). All other coefficients and terms including dl_n are evaluated at interation n. This notation is referred to as backward differencing. One might think that greater accuracy would be acheived if we used some form of centered differencing; i.e. if we wrote all the subscript-n factors as the average of values at n and n−1. The result would still be a straightforward equation for variables at n, although there would be more 'constant' terms from n−1. In practice, however, the simpler backward difference form is used because it quickly damps out small fluctuations arising from numerical instabilities.

Dynamic aging
In one-dimensional calculations (spherical symmetry) dynamic terms enter the equation of motion (what used to be hydrostatic equilibrium) when sequential 'hydrostatic' models no longer meet the conditions of static equilibrium. We will not discuss these terms further here.