remember dρ/dr is negative.
1. The Convective Instability Criterion
Convection is a process where energy is transported by advection
through the motions of blobs, or cells, of material; hot cells rising and
cool cells falling.
Following an argument by Schwarzschild, suppose we statistically
displace a blob from height z to z + dz.
If the blob experiences forces which keep it going, the fluid is
convectively unstable. If it experiences restoring forces,
the fluid is stable against convection.
Suppose also that the blob always moves more slowly than sound, so
it remains in pressure equilibrium with its surroundings (that is,
hydrostatic equilibrium is still a reasonable approximation for
the pressure variation with height).
Also suppose that the blob does not exchange energy with its surroundings.
It remains adiabatic, e.g. the entropy remains constant.
This supposition is not really true,
but energy exchange will not alter the instability criterion, just
the net rate of energy transport.
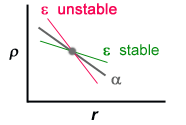
As the cell rises, it expands due to the pressure decrease. Now, if the cell becomes less dense than the surrounding medium, it becomes buoyant and rises further; the region is unstable. Label the cell ε, and the ambient medium α. Then the region is unstable if:
|
[dρ/dr]ε <
[dρ/dr]α . remember dρ/dr is negative. |  |
But, our basic equations include the temperature gradient [main carrier of l(m)] and the pressure gradient (hydrostatic equilibrium). At constant pressure, an increase in temperature results in a decrease in density, so we may equally well write the above criterion as
|
[dT/dr]ε >
[dT/dr]α . remember dT/dr is also negative. | 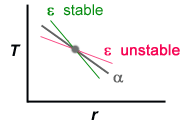 |
Adiabaticity is hard to figure on a radial gradient. Elements move very subsonically so we may assume pressure equilibrium; i.e. both element and ambient have the same pressure gradient, so we may multiply both sides of the inequality by dr/dP (a negative quantity) to state:
|
[dT/dP]ε <
[dT/dP]α or, in logarithmic terms, [d lnT/d lnP]ε < [d lnT/d lnP]α . | 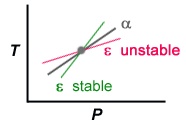 |
But remember that
(d lnT /d lnP) ≡
(Γ2−1)/Γ2 ≡ ∇,
and that we are assuming the element is adiabatic.
So we may write the instability criterion as
∇A < ∇α .
For a perfect gas, Γ2 = 5/3, so ∇A = 0.4. For a photon gas (e.g. radiation pressure dominates), Γ2 = 4/3 and ∇A = 0.25. In a region where hydrogen is partially ionized, Γ2 ∼ 1.1, because as the gas expands and cools it recombines and releases latent heat of ionization. This heat keeps it hotter than a perfect gas, making it more buoyant. The same effect occurs in Earth's atmospheric convection, where the latent heat is extracted from water condensation.
In radiative and hydrostatic equilibrium, in the diffusion limit
∇α =
[3 κ P l(m)] /
[16πacG m T 4] ≡
∇rad ,
where l(m) is the luminosity at m and κ is the
Rosseland mean opacity.
Where hydrogen and helium are partially ionized, κ is high and T is fairly low, so ∇rad >> ∇A = 0.1 and convection is vigorous.
For stars fusing hydrogen via the CNO-cycle (M > 1.3Mo), The nuclear energy generation is very temperature-sensitive, so most of the luminosity is generated within a small m core region. That centrality raises ∇rad and drives core convection.
While the criterion for convective instability is sufficient, it is not necessary. The form of convection results in rapidly moving elements which, on coming to the boundary of stability, are still out of equilibrium with the ambient region. These elements will continue to rise (or fall) through a stable region until buoyancy equilibrium is achieved. Thus, near a convectively unstable region are boundary layers where individual cells penetrate.
2. Mixing-Length Theory
The so-called mixing-length theory of convection is a local, diffusive
theory which may or may not be a good approximation in the stellar
envelope, and is decidedly bad in a stellar atmosphere.
But, once again, thinking about the concept of a mixing length helps to
understand the nature of convection and the real problem of its treatment.
The mixing length is defined as the distance
L an average cell travels
up or down before it `deposits' its energy content; e.g. before it becomes
indistinguishable from its environment.
In fact, this is not the right way to think about how convection works
in stars.
It might be OK for isolated thunderstorms.
In stars, where the average convective flux is constant over a horizontal
surface, the real tendency (according to recent numerical simulations)
is for the region as a whole to rise more-or-less uniformly,
while being threaded by narrow streams of cold downward flowing gas.
The downflowing streams compress to ribbons and fall at nearly the speed
of sound. They penetrate into stable regions below, spread out and heat
up, extracting energy from the surroundings. The continual flow of heavy
cool material into the interior pushes up the ambient warm material.
Never-the-less, let us proceed.
At any one time (so the story goes), about half of the surface is rising and half is falling (more like 90%$ up, 10% down). The rising blobs continue until they have expanded to fill the entire volume (not very consistent, but you get the picture). Then they become the new medium out of which new blobs form.
Thus, the cells are likely to travel approximately one pressure scale height.
Consider lots of gradients ∇rad, ∇α, ∇ε, and ∇A. In general,
∇rad > ∇α > ∇ε > ∇A
in unstable regions.
Approximate the situation with cells moving with speed v and internal energy difference ρΔU ergs/cm 3. Then the convective flux is just Fcond = v ρΔU = v ρ CPΔT, where CP is the specific heat at constant pressure. So what are ΔT and v?
ΔT = [(dT/dr)ε − (dT/dr)α] Δr,
where Δr is the average distance over which the blob has traveled since detaching from the ambient medium, Δr = L /2. We can convert the temperature gradients to ∇'s through hydrostatic equilibrium:
dP/Pdr ≡ −1/H,
the pressure scale height. Thus:
ΔT = (1/2) T (∇α − ∇ε) L /H .
We have assumed that CP is constant over one scale height, and neglected any variation in μ.
To find v, we ask what are the buoyant forces and for how long have they been acting on the cell? The work done on the cell is W = ∫ Fb dr over the path of the cell. Set W = v 2/2 (note that both W and Fb are per unit mass). The buoyant force Fb = −gδρ/ρ = gQδT/T in pressure equilibrium where δP = 0. Here Q ≡ − (∂lnρ /∂lnT)P .
Now assume δT is linear with displacement, so:
∫ Fb dr = gQ (ΔT/T )Δr/2 = gQH (∇α − ∇ε) (L /H ) 2/8 .
So
v 2 = gQH (∇α − ∇ε) (L /H ) 2/4 .
and for the flux,
Fconv =
(gQH )1/2
ρCP T
(∇α − ∇ε)3/2
(L
/H ) 2/4 .
This formula (from Mihalas) differs from H&K by the /4.
But, we still don't know ∇ε very well. We can try to guestimate it in terms of ∇α and ∇A which we do know. As the cell rises, it tends to lose energy to the surroundings via radiation (also entrainment, which is more important in real convection at depth). At this point, we can (and everyone does) make any choice we want, because all are going to be inaccurate. Mihalas describes a weighted average between optically thin and optically thick radiation limits, which does not include entrainment. We could just as well assume that ∇ε = (∇α + ∇A) /2.
This formula for the total flux contains the ratio L /H as a single parameter for characterizing the convection efficiency. The radius of the sun ultimately depends on three unknowns: the mixing-length, the age, and the helium abundance. We think we know the age and the nuclear reaction rates (assuming the 'solar neutrino problem' has been solved). Using typical B-star helium abundances results in L /H ≈ 2.
The mixing-length description has enjoyed a long and fruitful history. While it may not decribe the details of convection very well, it is a simple phenomenological approach which at least transports flux with the right order of magnitude. No other one-dimensional theory is better. All have disappointing ad hoc assumptions or parameters. Only three-dimensional numerical simulations are an improvement, but they suffer from simplistic radiative transfer and an inability to include the smallest and the largest scales, both of which may be important.
Professor Bob Stein at MSU has good material on numerical convection.
3. So how do we use the above equation for the convective flux?
The luminosity l(m) = 4πr 2(Fconv+Frad) must be the sum of all energy generated inside m. If ρCPT is large (interior convection) then even a very small ∇α − ∇ε will carry all the flux needed. Since the energy content is high and there is very little exchange between the convective cells and the ambient medium, both are very close to ∇A. Thus for efficient convection we may write simply that the temperature gradient is the adiabatic gradient:
P dT/dm = T (1−1/Γ2) dP/dm.
Most authors use γ for Γ2.
The convection carries whatever luminosity is required with very small superadiabaticity. Such a convective region is essentially transparent to the luminosity, and carries it out on dynamic time scales. It will turn out that radiation still carries some of the flux since there is a gradient.
Near the surface of a star, ρCPT becomes low, so the convection becomes inefficient and the element gradients depart from the ambient gradient. Both become quite superadiabatic, and the radiant flux competes with the convection. We can use this competition to calculate ∇α − ∇ε. Then, if we have an expression for the rate of energy exchange between the convective elements and their environment [for example, the simple expression ∇ε = (∇α + ∇A) /2 ], we can deduce the environmental gradient.
l(m) = 4πr 2 (gQH )1/2 ρCP T (∇α − ∇ε)3/2 (L /H ) 2/4 + (16πacG m T 4)∇α /(3 κ P).
Unfortunately a calculated stellar radius depends rather strongly on the choices made for describing the energy losses from a convective element if there is inefficient convection just under the surface of a star. All one-dimensional calculations suffer from this problem. Such models must have 'adjustable parameters' that may be set to reproduce known stellar radii.