The usual graph of binding energies per nucleon as a function of the mass number A:
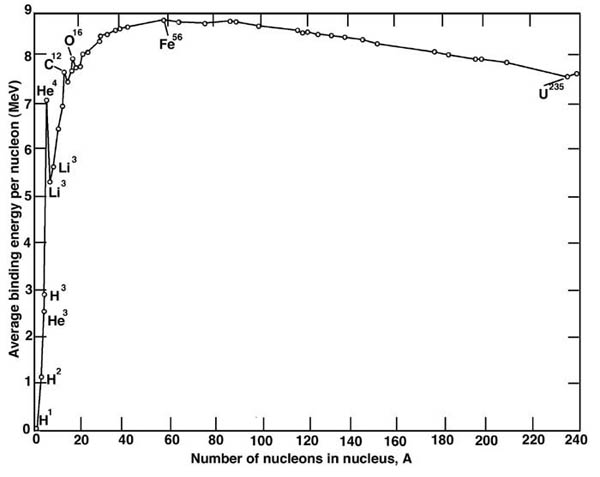
For example:
Total BE of 4He is 4 × 7.074 = 28.3 MeV,
total BE of 12C is 12 × 7.680 = 92.2 MeV, so
3 (4He) − 12C = 7.26 MeV, a typical Q-value.
1. Gravitational energy
The expression for the gravitational energy generation per gram of material
is deceptively simple:
εgrav = − dQ /dt =
− [dE /dt + Pd(1/ρ) /dt]
Q: Heat added per gram
E: Internal energy per gram
and the derivatives are understood to be Lagrangian, e.g. following the matter
(automatic on a mass scale).
Mushing things about with thermodynamic identities and adiabatic coeficients, we may write in terms of our model state variables:
εgrav = − [P/ρ(Γ3 − 1)] [d lnP/dt − Γ1 d lnρ/dt] .
At first, this expression seems not useful, because we are used to thinking 'what is the temperature profile if ε is such-and-such?' How are we to determine the time derivatives as functions of P and T? This thinking is the wrong approach. Instead, we should think of this equation as 'how the state variables will change with time if the local divergence of the flux is so-and-so'. Somewhere there must be a divergence of flux. The surface radiates l(m) = L, and l(m) = 0 at the center. Time evolution evens out the divergence over m until a relatively steady structure is achieved. Ultimately, the logarithmic derivatives will try to equalize throughout the star; all the star must age at roughly the same rate. Such equality is called homologous change; all of the layers change in proportion. Gravitational collapse is time-dependent at its core, despite these relatively stable configurations.
In radiative regions, the divergence of flux is controlled by the opacity. Very opaque regions will insulate the interior, preventing transport so luminosities will be low and time rates of change will be long.
In convective regions, things are different. Remember that the adiabatic gradient says nothing about flux or flux divergence. Technically, a purely adiabatic region cannot transport flux at all, but a slight super-adiabaticity can carry nearly infinite flux if necessary. Thus, in regions of efficient convection the structure remains very nearly adiabatic. εgrav is determined by the global contraction/expansion controlled by the radiative surface and/or other radiative regions.
2. Nuclear Reactions
1. Introduction
General process: α + X → Z* → Y + β,
xxxx or X(α,β)Y .
α, X, Y, β : nuclear species,
Z* : intermediate, short-lived, usually excited, compound nucleus.
α, β are often smaller particles such as
α n p e ν γ, etc.
The intermediate Z* often has many decay channels Y + β.
Nuclear reactions are usually treated with the same formalisms used for atomic excitation/ionization/recombination/molecular reactions; e.g. cross sections, lifetimes.
For an excited state, the natural width
Γi = ΔEi =
(h/2π) / τi
[(1/τi) ≡ Aji in atomic transitions.]
2. Energetics
Total binding energy: energy required to disperse all nucleons to infinity.
The usual graph of binding energies per nucleon as a function of the mass number A:

For example:
Total BE of 4He is 4 × 7.074 = 28.3 MeV,
total BE of 12C is 12 × 7.680 = 92.2 MeV, so
3 (4He) − 12C = 7.26 MeV, a typical Q-value.
Radii: R ≈ 1.4 A1/3 femtometers.
Minimum interparticle separation: D ≈
1.4 (Aα1/3 + AX1/3) fm.
Coulomb barrier: Zα ZX e 2 / D ≈ 1 MeV.
3. Cross sections and rates
The fuzzy quantum mechanical process is treated in bulk with cross sections:
Total rate in interval dv : Rαβ(v) dv =
nα(v)dv σαβ(v) v nX
cm−3s−1,
where v is the relative speed in the rest frame of the α-X center of mass.
We may write the rate integrated over all speeds as
Rαβ = ∫ nα(v) σαβ(v) v nX dv = nα nX <σv>αβ cm−3s−1,
partly for convenience and partly because usually the range of thermal kintetic energies is small relative to the energy range of nuclear excitations.
The Maxwell distributrion function of kinetic energies is:
nα(E)dE = nαΨ(E)dE = nα (2/√π) (kT)−3/2 e−E/kT E 1/2 dE ,
normalized so ∫Ψ(E)dE = 1.
Non relativistic, E = mv 2/2.
So,
<σv>αβ =
(8/πm)1/2(kT)−3/2
∫σαβ (E) e−E/kT E dE
cm−3s−1,
m = mαmX/(mα + mX).
The usual expression for σαβ (E) is
σαβ (E) = π (λ/2π)2
g (ΓαΓβ /Γ2)
f (E),
π (λ/2π)2 = π(h/2π)2/2Em =
0.657/Eμ barns (the 'deBroglie cross section'); E in MeV, μ reduced mass in AMU.
g : statistical weight factor.
(ΓαΓβ /Γ2) :
joint probablility of α-channel in, β-channel out.
f (E) : profile function; resonant and/or non-resonant.
Resonant reactions
The compound nucleus Z* has a discrete energy state E* so the energy equation reads
mZ*c 2 + E* = mαc 2 + mXc 2 + Er ,
and the kinetic energy range significantly overlaps Er. For well-separated nuclear states, f (E) becomes the Breit-Wigner (Lorenzian)
f (E) = Γ2/[(E − Er)2 + (Γ/2)2].
If we assume that the width of the resonance Γ is much narrower than any variations of other terms over energy, we may replace those other terms with their values at Er, and carry out the integral of f (E) to get
<σv>αβ = (h/2π)2 (2π/mkT)3/2g (ΓαΓβ /Γ ) e−Er /kT.
The expression g (ΓαΓβ /Γ ) is written (ωγ)r by Fowler, et al. and tabulated for many reactions. Then
<σv>αβ = 2.56×10−13 (ωγ)r (μT9)−3/2 e−11.605Er /T9; ωγ and Er in MeV.
Expressing the above temperature dependance as a power law T ν, ν = (11.605Er /T9) − 3/2.
Homework: Show that the formula for the resonant <σv>αβ above is correct (i.e. integrate the profile) and that the power law exponent ν is correct.
Non-resonant reactions
When there is no energetically favorable resonance, the cross section takes the form
σαβ (E) = S(E ) e−2πη /E .
The 1/E factor comes from the deBroglie cross section,
The e−2πη factor comes from the Coulomb barrier penetration,
and the S(E ) contains all the other miscelaneous constants and weakly energy dependent factors.
Here η = ZαZXe 2/(vh/2π) = 0.1574 ZαZX (μ/E )1/2.
Substituting into the formula for <σv>αβ averaged over the Mawell distribution of speeds gives
<σv>αβ = 1.6×10−15
μ−1/2 (kT)−3/2 So
∫ exp[ − (E/kT + b/E1/2)] dE
cm3s−1,
with b = 0.99 ZαZX μ1/2.
Everything is in AMU and MeV. So is the value of S(E ) at Eo described below. The figure below shows the terms in the exponential, their sum, and a scaled to fit plot of the exponent function itself for the reaction p + 12C at T6 = 20.
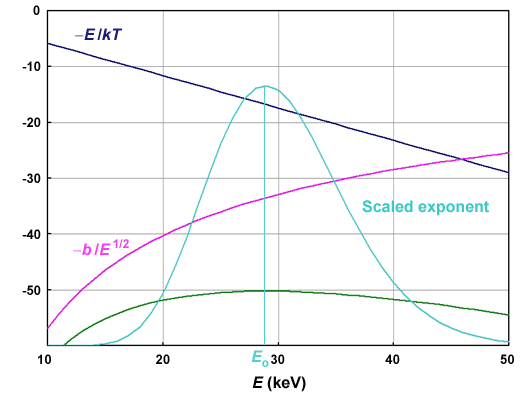
The exponent function forms a nearly Gaussian peak, called the Gamow peak.
The maximum is at
Eo = 1.22 (Zα2 ZX 2 μT62 )1/3 keV
and has a full-width at 1/e of maximum of about Δ ≈ 2.3 (EokT)1/2.
Assuming a Gaussian shape, the average rate becomes:
<σv>αβ = 0.72×10−18
So (μZαZX)−1
e−τ τ 2
cm3s−1,
τ = 3Eo/kT.
Expressed as a power law T ν,
ν = (1/3) (a T6−1/3 − 2),
a = 42.49 (Zα2
ZX 2 μ)1/3.
4. Summary
The rate for an αβ reaction is
Rαβ = ∫
nα(v) σαβ(v) v nX dv =
nα nX <σv>αβ
= ρ 2 NAv2
(Xα /Aα)
(XX /AX)
<σv>αβ
cm−3s−1,
where the X 's are the mass fractions.
The energy generation is
εαβ = Rαβ
Qαβ /ρ
erg g−1 s−1.
The energy generation is usually espressed as a power law,
ε = εo (ρ/ρo)λ
(T/To)ν,
λ = 1,
ν = (11.605Er /T9) − 3/2, resonant,
ν = (1/3) [42.49 (Zα2
ZX 2 μ)1/3
T6−1/3 − 2] non-resonant.
Reaction rates also contribute to abundance equilibrium and time rates of change equations, of course.
5. Electron screening
The presence of electrons lowers the Coulomb barrier, particularly at distances greater than the inter-electron distance. The electrons tend to cluster in the neighborhood of nuclei. An approximation for the reduction of the potential comes from Debye-Hückel theory:
φ(r) = (Ze /r)
e−r/rD,
rD = [(4πe 2/kT)
(Z 2nI + ne)] −1/2.
Various further approximations involving the classical turning radius rt = (Ze)2/EGamowPeak leads to a reduction of the barrier by Uo = (Ze)2/rD , which in turn increases the velocity-averaged cross section by a factor of eUo /kT. If this factor is significant, some care must be taken to do the screening right.
6. Specific cases
The proton-proton chain and deuterium burning
The CNO cycles
Helium burning
C, O, Ne, Si burning and photo-disintegration processes
Nuclear statistical equilibrium among the iron group