Outline

5. Radiative Energy Transport and Opacities

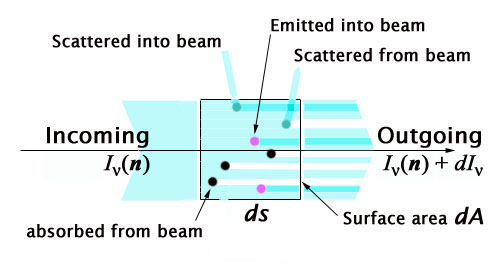
i. Variables.

Iν(n)	Radiation specific intensity ergs cm−2 sec−1 strdn−1 Hz−1
χν	Radiation extinction cm−1
ην	Radiation emissivity ergs cm−3 sec−1 strdn−1 Hz−1

A. Considerations.
The specific intensity I_ν(n) is the amount of radiant energy at frequency ν passing in a beam in the direction n, per unit frequency, per unit area, per steradian, per unit time. Thus:
I_ν(n) dν dA dΩ dt has units ergs (in cgs).

The intensity is reduced when the beam passes through absorbing particles and increased when the bean passes through emitting particles. Consider a beam passing through a volume dsdA containing different types of particles:

Because absorpion and emission are quantum mechanical processes, we may assume that upstream particles to not directly "shade" downstream particles, but only reduce/increase the average number of photons in the beam. None-the-less, there are enough particles in the volume that the probabilistic nature of the processes is not important, and we can assign cross sections to individual particles in a classical sense.

B. Terms in the Equation of Transfer.
The radiation energy coming into the volume within dΩ is
I_ν(n) dν dA dΩ ergs/sec.

The energy change due to absorption by particles in the volume is:
dI_ab dν dA dΩ = − I_ν dν dΩ dsdA n_aba_ab(ν),
where dsdA n_ab is the total number of absorbers in the volume, and a_ab(ν) is the cross section of each absorber. Thus we may write:
dI_ab = − n_ab a_ab(ν) I_ν ds.

Similarly, we may write for scattering out of the beam:
dI_sc = − n_sc a_sc(ν) I_ν ds.

Combining the above together, we have for the total extinction:
dI_ex = − χ_ν I_ν ds.

The energy change due to emission by particles in the volume is generally written as:
dI_em = η_ν ds,
where η_ν is the volume emissivity (see units above).

The emissivity has many parts:
Stimulated emission: usually included as a negative contribution to χ_ν, since it is proportional to I_ν and adds energy into the beam parallel to n.
Spontaneous emission: independent of I_ν.
Scattering: radiation scattered into the beam from other directions and/or frequencies.

C. The Equation of Transfer along the direction n.

∂ I_ν(n) /∂s_n = − χ_ν I_ν(n) + η_ν

In geometries with azimuthal symmetry, e.g. plane parallel or spherical, the specific intensity is independent of the azimuth angle and varies only with depth and the zenith angle θ.

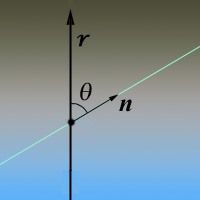
Let μ = cos(θ). Then ∂s_n = dr/μ and the transfer equation becomes

μdI_ν(r,μ) /dr = − χ_ν I_ν(r,μ) + η_ν.

D. Angular Moments of the Specific Intensity
and the Equation of Transfer

In the definitions below, both the general form and the azimuth symmetry form of the angular moments are given.

b. The Mean Intensity:

J_ν = (1/4π) ∫ I_ν(n) dΩ.
J_ν = (1/2) ∫ I_ν(μ) dμ.

c. The Eddington Flux:

H_ν = (1/4π) ∫ I_ν(n) n dΩ.
H_ν = (1/2) ∫ I_ν(μ) μ dμ.

In the general form, the Eddington flux is a vector. In the symmetric form, the flux is parallel to the radial direction.

The true energy flux is:
F_ν = 4πH_ν = l (r) /4&pir ².

d. The Eddington Stress:

K_ν = (1/4π) ∫ I_ν(n) nn dΩ.
K_ν = (1/2) ∫ I_ν(μ) μ ² dμ.

In the general form, the stress is a second rank tensor. For isotropic radiation, K is diagonal with equal elements and may be replaced with a scalar, as in the case of isotropic pressure.

The radiation pressure is:
P_ν = (4π/c)K_ν.

e. The equation of transfer.

Multiply by μ/2 and integrate over μ:
dK_ν /dr = − χ_ν H_ν.
Notice that since the emissivity is isotropic, the integration of μη over μ is zero.

E. The Diffusion approximation on the mass variable.

We may replace χ_ν, which is rather density dependent, with ρκ_ν, where κ_ν is the opacity in units cm²/gram.
Then by applying the continuity equation relating m(r) to r, we find

4πr ²dK_ν = − κ_ν H_ν dm.

Apply the diffusion approximation K_ν = J_ν/3 and the optically thick approximation J_ν = B_ν:
4πr ²dB_ν = − 3κ_ν H_ν dm.

Divide by κ_ν and integrate over ν:
4πr ² ∫ (1/κ_ν) dB_ν dν = − 3l(m) dm /16π²r ².

Now define the Rosseland mean opacity κ through:
∫ (1/κ_ν)dB_ν dν ≡ (1/κ) ∫ dB_ν dν = (1/κ) acT ³dT/π.

Finally, then:
64π ²r ⁴acT ³dT = − 3κ l(m) dm

5.2. The Surface Boundary Condition
Consider stars with radiative envelopes below the surface (e.g. T_eff > 8000 K). The temperature mass gradient will be
dT/ dm = − 3κl /64π ²r ⁴acT ³
Opacities will always be of the order of 1 cm ²/gram. Consider a 5 Solar-mass star, with T_eff ∼ 13000 K. The gradient, in Solar-mass units, becomes:
dT/ dm ∼ 7×10¹² deg/Solar-mass,
which is so steep that the calculation does not really know the difference between 13000 K and zero K. This result is called the radiative zero condition. The effective temperature of the calculated star is then determined from the surface luminosity and radius.

5.3 Opacities

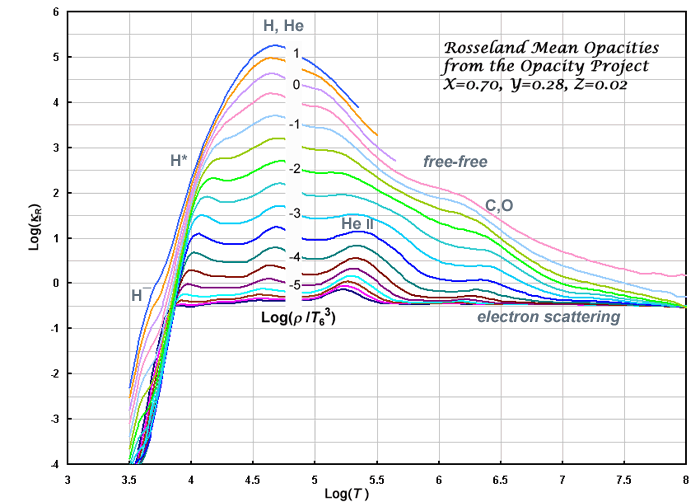
The best Rosseland opacities are from either the Opacity Project or the OPAL Project. These opacities (and equation of state) appear in two-dimensional tables [κ (logT, logR) where R=ρ/T₆³] for a given composition. One problem; while one might imagine a finite number of tables with various ratios of X /Y, and/or ratios Y /C+O, nuclear evolution results in almost infinite variations in composition. There is no easy way to account for each opacity source independently due to the electron number.

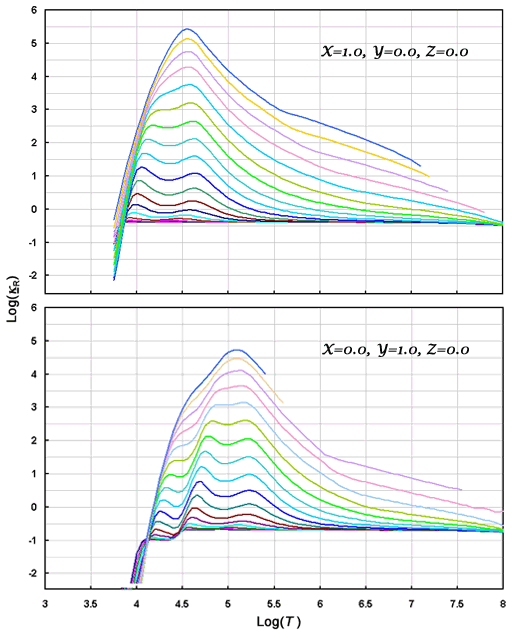
Notice that nearly full ionization (as recorded by the electron scattering contribution) occurs 0.5 or more in log(T ) earlier than the opacity peak, which occurs when the Planck function moves over the ionization edge of the remnant un-ionized population.