T(ξ) = Tc θ(ξ) with
(n + 1) (−ξθ′ )ξ1 Tc = (Gμ/NAk) M /R = 2.293×107 μ (M/Mo) (Ro/R) K.
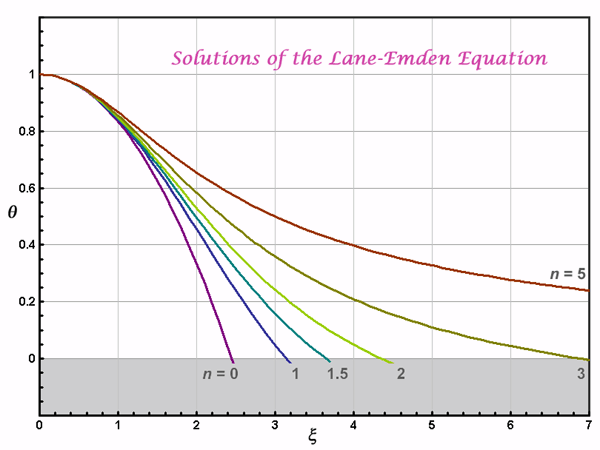
Analytic solutions are only possible for n = 0, 1, and 5.
dm/dr = 4π r 2ρ
(r 2/ρ) dP/dr = −Gm .
Take the derivative of the HE equation and substitute continuity to get
(1/r 2) (d/dr) [(r 2/ρ) dP/dr] = −4πGρ.
If we had an expression for P = f (ρ), we could solve this Poisson equation
directly (albeit numerically).
A polytropic star is one where the pressure varies as the density to some power over
the radial position.
Keep in mind that the local gas itself may or may not obey some γ-law equation of
state; the variation we are speaking of here is the relation between P and ρ
point-to-point along the radial direction.
Assume P(r) = Pc [ρ(r) /ρc]1+1/n
where the 'c' subscript refers to central values.
Note: n is the polytropic index, not any of the other uses of the symbol we have seen.
H&K, and most other writers following historical writings, use
P(r) =
K ρ1+1/n(r).
However, I don't like raising dimensioned quantities to arbitrary powers.
Anyway, we will scale the density everywhere by the central density in the following
manner:
ρ(r) ≡ ρc θ n (r),
so P(r) = Pc θ n+1 (r) .
The Poisson equation becomes
[(n + 1)Pc /4πGρc2] (1/r 2) (d/dr) [r 2 dθ/dr] = −θ n.
Now scale the radial dimension as r 2 ≡ [(n + 1)Pc /4πGρc2] ξ 2 ≡ rn2ξ 2, so the Poisson equation becomes the dimensionless
(1/ξ 2) (d/dξ) [ξ 2 dθ/dξ ] = −θ n.
This equation is known as the Lane-Emden equation.
We require two boundary conditions to solve a second-order differential equation.
For stars, the obvious choices are
θ = 1 at ξ = 0, and
θ′ = dθ/dξ = 0 at ξ = 0.
Then the surface of the star 'happens' when θ (ξ) = 0,
which in turn is when ξ = ξ1.
From the continuity equation m(r) =
∫0r
4π r 2ρ dr,
m(ξ) =
4π rn3ρc
∫0ξ
ξ 2θ ndξ =
−4π rn3ρc
ξ 2dθ/dξ ,
so M = 4π rn3ρc
(−ξ 2θ′ )ξ1 .
Lots of algebra results in
4π(n + 1) θ′ξ12
Pc =
GM 2/R 4
ρc /ρ = (1/3)
(−ξ /θ′ )ξ1 where
ρ is the mean density, and
Ω = −[3/(5 − n)] GM 2/R .
For the ideal gas equation of state,
T(ξ) = Tc θ(ξ) with
(n + 1) (−ξθ′ )ξ1
Tc =
(Gμ/NAk) M /R =
2.293×107 μ
(M/Mo) (Ro/R) K.

Analytic solutions are only possible for n = 0, 1, and 5.
| n = 0: | θ = 1 − ξ 2/6 | ξ1 = √6 | θ′ξ1 = −√6 /3 | Constant density |
| n = 1:x | θ = (1/ξ ) sin ξ | ξ1 = π | θ′ξ1 = −1/π | |
| n = 1.5:x | ξ1 = 3.6538 x | θ′ξ1 = −0.20330 x | Non-relativistic degeneracy and ideal convection | |
| n = 2:x | ξ1 = 4.3529 | θ′ξ1 = −0.12725 | ||
| n = 3:x | ξ1 = 6.8969 | θ′ξ1 = −0.04243 | Relativistic degeneracy and the 'Eddington standard model' | |
| n = 5: | θ = (1 + ξ 2/3)−1/2x | ξ1 = ∞ | θ′ξ1 = 0. | Note: the mass is finite although the radius is infinite. |
Zero-temperature white dwarfs
We may write the central density as ρc = (1/3)
(−ξ /θ′ )ξ1 ρ =
(−ξ /θ′ )ξ1
M /4πR 3.
With the formula for Pc above and the various degenerate equations of state
Pe = 1.004×1013
(ρ/μe)5/3 in the non-relativistic limit (n = 3/2)
Pe = 1.243×1015
(ρ/μe)4/3 in the relativistic limit (n = 3)
we can derive mass-radius relationships:
(R /Ro)3 =
2.08×10−6 (2/μe)5
(M /Mo)−1 non-relativistic,
(M /Mo) = 1.456 (2/μe)2 relativistic.
(The 2 is included with the μe because μe ≈
2 for fully ionized gasses other than hydrogen.)
In the relativistic analysis, the radius cancels out leaving only one mass value. One may interpret this result to mean that as the mass approaches this value the electrons become more and more relativistic, and the radial configuration becomes less significant; i.e. the star may exist at any radius and change radius without changing potential or doing work. Since gravity is still present, it collapses. This critical mass is the Chandrasekhar limit and is usually notated M∞ referring to its ultimate density.
A good formula for both regimes (Eggleton) is R /R1 = 2.02 [ 1 − (M /M∞)4/3]1/2 (M /M∞)−1/3 where R1 = 1.117×10−2Ro /μe .
Homework: work out the above mass-radius relationships for white dwarfs.