Outline

10. Star aging

1. Main sequence

The "four" equations for stellar structure assuming quiescent aging again:

4πr ²ρdr = dm

dl = ε dm
Gravitational and Nuclear energy generation: ε = ε_o (ρ /ρ_o) ^λ (T /T_o) ^ν

4πr ⁴dP = −Gm dm
Equation of State: P = P_o (ρ /ρ_o) ^β (T /T_o) ^α

Radiative layers
64π ²r ⁴ac T ³dT = − 3κ l dm
Mean opacity: κ = κ_o (ρ /ρ_o) ⁿ (T /T_o) ^−s

Convective layers
P dT = T(1−1/γ) dP

Consider two stars on the zero-age main sequence with slightly different masses M = M_o + δM, and write the variables as:
y(m/M) = y_o(m/M_o) + (∂y/∂M) δM = y_o(m/M_o) [1 + (∂ln y /∂M) δM].

Substitute into the equations (illustrating only the radiative set):

4πr_o ³ [1 + 3 (∂ln r /∂M) δM] ρ_o [1 + (∂ln ρ /∂M) δM] d ln r = m_o [1 + (∂ln m /∂M) δM] d ln m
l_o [1 + (∂ln l /∂M) δM] d ln l = ε_o [1 + (λ ∂ln ρ /∂M + ν ∂ln T /∂M) δM] m_o [1 + (∂ln m /∂M) δM] d ln m
4πr_o ⁴ [1 + 4 (∂ln r /∂M) δM] P_o [1 + (β ∂ln ρ /∂M + α ∂ln T /∂M) δM] d ln P = Gm_o² [1 + 2 (∂ln m /∂M) δM] d ln m
64π ²r_o ⁴ [1 + 4 (∂ln r /∂M) δM] ac T_o⁴ [1 + 4 (∂ln T /∂M) δM] d ln T =
xxxx − 3κ_o [1 + (n ∂ln ρ /∂M − s ∂ln T /∂M) δM] l_o [1 + (∂ln l /∂M) δM] m_o [1 + (∂ln m /∂M) δM] d ln m .

Now assume homologous behavior; i.e. the partials ∂ln y /∂M are independent of m. Then the logarithmic derivatives d ln y /d ln m are independent of M and all factors containing constants (and y_o's) cancel because we know that the y_o's satisfy the equations. If we keep only terms linear in δM, δM also drops out. We are left with four equations in the four unknowns ∂ln y /∂M, which we can express as the vector equation

x3x	0	1	0		∂ ln r		1
0	x1x	− λ	− ν		∂ ln l		1
4	0	xβx	xαx	x•x	∂ ln ρ	x=x	2	∂ lnM
4	− 1	− n	4 + s		∂ ln T		x1x

The solution is:

∂ ln r /∂ lnM = (1 − x/D) /3
∂ ln l /∂ lnM = 1 + (λ x − ν z) /D
∂ ln ρ /∂ lnM = x /D
∂ ln T /∂ lnM = − z /D,
where
x = 2 (α + ν − s − 4)
z = 2 (β + λ + n)
D = (3β − 4) (ν − s − 4) − α (3λ + 3n +4).
[Assuming re-ordered equations, multiplying one by −1, and that H&K have done their algebra right on p. 25.]

Since these derivatives are assumed independent of m, we may assume that they represent values of
∂ ln R /∂ lnM
∂ ln L /∂ lnM
∂ ln ρ_c /∂ lnM
∂ ln T_c /∂ lnM,
the unknown boundary values.

Assume
λ = 1, ν = 18; (CNO burning)
β = 1, α = 1.2; (perfect gas law + some radiation)
s = 1.5, n = 0.3; (electron scattering + some ionization).
Then

∂ ln R /∂ lnM	=	0.75	0.7
∂ ln L /∂ lnM	=	3.52	3.5
∂ ln ρc /∂ lnM	=	−1.25	−1.3
∂ ln Tc /∂ lnM	=	0.21	0.2

The bold numbers describe the 'real' upper main sequence, so the estimation is not far off. Of course, the power exponents were adjusted to make the match; however, the values are reasonable. A little experimentation will show that the derivatives are quite sensitive to the values of the exponents, particularly β, α, and n.

2. Semi-convection

For stars more massive than 10M_sun, the core convection grows in m as hydrogen is depleted, producing a discontinuity in X.

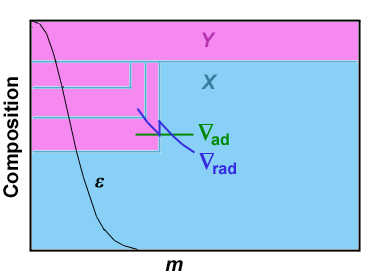
The adiabatic gradient is virtually continuous across the discontinuity. The radiative gradient ∇_rad = (3 κ P l ) /(16πacG m T ⁴) decreases outward mostly proportional to 1/m (l is already ≈ L), and full convection stops when it drops below ∇_ad. Both P and T are continuous across the discontinuity. However, κ ≈ 0.2 (1 + X ) becomes discontinuous due to the discontinuous electron-to-baryon ratio. Therefore ∇_rad is higher in the unprocessed envelope. Convection will procede until ∇_rad is reduced to ∇_ad by mixing in some helium and smoothing out the discontinuity. Nuclear evolution chews into the bottom edge, maintaining the smoothing convection in a marginal state called semi-convection. Semi-convection is very difficult to treat. The amount of hydrogen it feeds into the core significantly affects the total fuel available on the main sequence.

3. Post main sequence

Why does a star move in one direction (generally L increases slowly by a factor of 2 to 3, and T_e decreases by about 25%) on the main sequence, and then suddenly expand with decreasing surface temperature at some point? What triggers the rapid transition? Why doesn't the star stay near the main sequence as it consumes hydrogen in a shell around a helium core?

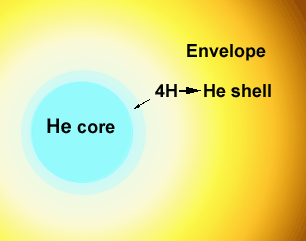
The virial theorem and homology argue for a maximum He core mass of about 0.08M above which stable nuclear aging is no longer possible.

Assume an isothermal core at a temperature maintained by the hydrogen burning shell right above it. As long as the system is stable, the nuclear reactions will provide an effective thermostat. The virial theorem for a core with outside pressure is

2K + Ω = 3P_sV,

where P_s is the core surface pressure and V is the volume. Substitute

2K = 3 (M_cN_Av /μ_c ) kT_c
Ω = − (3/5) GM_c²/R_c
V = 4πR_c³/3

and solve for P_s

P_s = (3/4π) (M_cN_Av /μ_c ) kT_c R_c⁻³ − (3/20π) GM_c² R_c⁻⁴

In the event that the core becomes (non-relativistically) degenerate, we may add a term
P_e = 1.004×10¹³ (4π μ_e /3)^−5/3 M_c^5/3 R_c⁻⁵.

in solar units:
P_s = 11.6×10¹⁴μ_c⁻¹ T₇ M_c R_c⁻³ − 5.38×10¹⁴ M_c² R_c⁻⁴ [ + 5.60×10¹² M_c^5/3 R_c⁻⁵]_Rc<0.03.

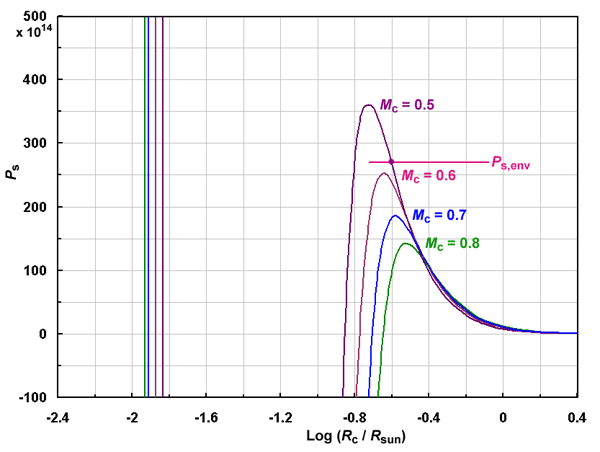
The following figure shows the form of P_s as a function of R_c for various M_c at the typical values T₇ = 2.2 and μ_c = 4/3.

Now consider the envelope. If we assume that the core is relatively small, we may estimate interior conditions from the polytropic relations:

4π(n + 1) θ′_ξ1² P_s = GM ²/R ⁴
(n + 1) (−ξθ′ )_ξ1 T_c = (Gμ_env/N_Ak) M /R .
Assuming n = 3 ('Eddington standard model') and solar units,
P_s = 1.24×10¹⁷ M ²/R ⁴
T_c = 1.96×10⁷ μ_env M /R .
Substuting from the second relation into the first gives:
P_s = 8.42×10¹⁵ μ_env⁻⁴ T₇⁴ M ⁻².

Assuming T₇ = 2.2, μ_env = 0.62, and M = 7, P_s = 272×10¹⁴. This value is marked on the figure with a horizontal line, since it is 'independent' of core values.

Then, aging on the main sequence continues as long as the core mass M_c remains small enough that the peak from the virial theorem configuration remains higher than the envelope pressure. The surface pressure solution is at the crossing of the two curves, marked with a dot. As the core grows, the virial peak drops. At a critical mass, the envelope heating can no longer sustain the internal pressure of the core, and the core then begins to collapse on a Kelvin-Helmholtz timescale to either degeneracy or the ignition of the 3-α process, which ever comes first.

We can find that critical mass by evaluating the derivative of the virial formula with respect to R_c, setting it to zero to find R_max, substituting this value into the virial formula to find P_max, and then setting that equal to P_{s, env}.

dP_s/dR_c = − 34.8×10¹⁴μ_c⁻¹ T₇ M_c R_c⁻⁴ + 21.5×10¹⁴ M_c² R_c⁻⁵ = 0.
so
R_max = 0.618 M_c μ_c T₇⁻¹, and
P_max = 12.3×10¹⁴μ_c⁻⁴ T₇⁴ M_c⁻².

Setting P_max = P_{s, env} and solving for M_c gives

M_c = 0.38 (μ_env /μ_c)² M.
A more accurate solution with realistic stellar modeling leads to

M_c = 0.37 (μ_env /μ_c)² M, called the Schönberg-Chandrasekhar limit.
[Note: such close agreement is fortuitous and results from including the (3/5) coefficient in Ω. The results are very sensitive to the relative strengths of the virial terms.]

Filling in the stated values for the molecular weights gives
M_c = 0.080 M.