The 8Be resonance lies 91.78 keV above separate α-particles.
Temperatures near T6 = 120 are required to make
the Gamow peak Eo =
1.22(Zα4μ
T62)1/3 = 92 keV.
Thus, helium-helium reactions will not take place while any protons are
still available.
Below is an energy-level diagram of reactants involved in the 3α process.
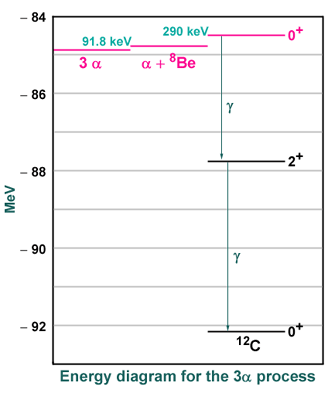
The γ decay (and/or electron-positron emission) from the excited resonance of
12C* is a very small leak compared to the exchange rates
3α ↔ α+8Be ↔ 12C*.
Therefore we may consider those three levels to be in statistical equilibrium,
and write the abundance of the 12C* level with respect to 4He
via two nuclear Saha equations (the statistical weights g = 1 for all three
species).
The rate for creating ground-state 12C out of 3α becomes
R3α =
nC*
Γrad 2π/h,
where Γrad is 3.67 meV.
The energy generation becomes (as quoted in H&K)
ε3α =
5.1×108ρ2 Y 3
T9−3 e−4.4027/T9
erg g−1 s−1.
The power law exponents are
λ = 2 and ν = 4.4/T9 − 3, ≈ 41 for
T9 ≈ 0.1.
The steep temperature dependence leads to explosive events, since the temperature may
rise on timescales shorter than the dynamic timescale.
Screening and other effects have not been included in the above formulae; see Fushiki and Lamb (1987, ApJ, 317, 368).
Further alpha reactions
The reactions 12C (α,γ) 16O and
16O (α,γ) 20Ne take place simultaneously
with the 3α process, although the latter is fairly slow at 3α
temperatures.
The former reaction determines the cosmic and white dwarf C/O ratio.
The rate for the carbon burning reaction is historically uncertain.