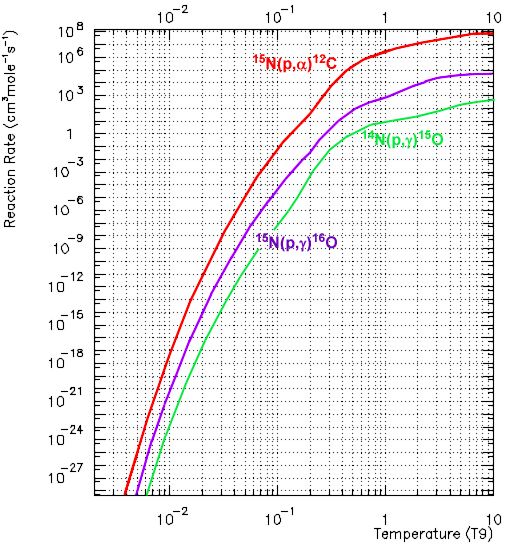
Plots from Caughlan and Fowler (1988).
| Q MeV | ν-loss MeV |
Decay time |
|||
| 12C + 1H | → | 13N + γ | 1.944 | ||
| 13N | → | 13C + e+ + νe | 2.221 | 0.71 | 870 s |
| 13C + 1H | → | 14N + γ | 7.550 | ||
| 14N + 1H | → | 15O + γ | 7.293 | ||
| 15O | → | 15N + e+ + νe | 2.761 | 1.00 | 178 s |
| 15N + 1H | → | 12C + 4He | 4.965 | ||
| or | → | 16O + γ | 12.126 | ||
| 16O + 1H | → | 17F + γ | 0.601 | ||
| 17F | → | 17O + e+ + νe | 2.762 | 0.94 | 95 s |
| 17O + 1H | → | 14N + 4He | 1.193 |
When a proton combines with 15N the compound is excited 16O*, which decays by the α-channel about 1000 times more frequently than by the γ-channel.

Plots from
Caughlan and Fowler (1988).
The slowest reaction is 14N (p,γ)15O, so in equilibrium almost all C, N, and O nuclei are converted to 14N (This equilibration is the main source of 14N; the reason there is more cosmic C and O is the result of the 3α process). However, the equilibration of the reactions is fairly slow, particularly from the oxygen segment of the cycle.
Homework: another numerical problem
Write each statistical equation as
dxn /dt = ρ
xn−1
xp
<σv>*n−1→n − ρ
xn
xp
<σv>*n→n+1
[note- the reactions which eject an α introduce different terms]
and
dxp /dt = −
ρ xp
∑n xn
<σv>*n→n+1 .
Here xn = Xn/An, and
<σv>*αβ = NAv
<σv>αβ, which is the quantity published by
Caughlan and Fowler (1988).
Assume that the beta decays are instantaneous; i.e., write the first reaction as
12C + 1H → 13C + γ + e+ + νe,
with a total Q = 3.455 (after neutrino losses), etc.
Assume T9 = 0.025, ρ = 100 (typical values for CNO-cycle burning).
Notice that the <σv>* values depend only on temperature so only need to be
calculated once.
Define a time interval Δt as
0.01×minimum(d ln xn /dt)−1.
Now write the time dependent equations as
xn(new) = xn(old) + Δt [
ρ
xn−1
xp
<σv>*n−1→n − ρ
xn
xp
<σv>*n→n+1 ]
xp(new) = xp(old) − Δt [
ρ xp
∑n xn
<σv>*n→n+1 ].
Start with the following mass fraction abundances attributed to the
pre-solar nebula (note X, not x;
from Lodders 2003, Ap.J., 591, 1220):
| Isotope | X |
| 21H | 7.11−1 |
| 12C | 2.46−3 |
| 13C | 2.98−5 |
| 14N | 7.96−4 |
| 15N | 3.13−6 |
| 16O | 6.60−3 |
| 17O | 2.62−6 |
Advance time in units of Δt and follow:
a) the abundance fractions x and
b) the energy generation ε.
Continue until some form of equilibrium among the CNO fractions is reached,
or one runs out of hydrogen (e.g. Xp < 0.1)
Re-evaluate the minimum Δt with each time step; as the abundances
approach equilibrium, the time steps become larger.
You should also continually check to see that
∑nxCNO
remains constant, and re-normalize to ensure that constancy. The xn
values are proportional to the number densities nn.
You may wish to use some better numerical receipe for the time advancement;
a simple correction is to iterate once or twice each time step, replacing the
values used to calculate the time derivatives with an average of the new and
old values.
You may also want to try smaller time steps to see if the result is the same.
As an added bonus, you may wish to adjust the temperature in each time step to maintain constant ε; only very small changes will be necessary, easily determined by evaluating the power-law dependence.
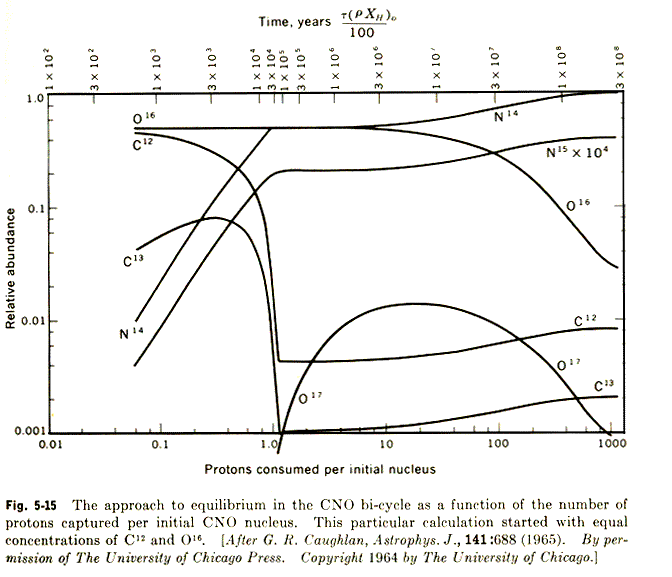
Your result should look something like this graph taken from Clayton's book,
Principles of Stellar Evolution and Nucleosythesis.
H&K give an estimated energy generation rate
εCNO = 4.4×1025 ρXZ T9−2/3 e−15.228/T91/3 erg g−1 s−1.
How does that estimate compare witht the calculations in the homework?
The temperature power law index becomes
νCNO = 50.8T6−1/3 − 2/3, which = 16.7 at T6 = 25.
Similar cycles repeat further along the periodic table, as illustrated in the following figure:
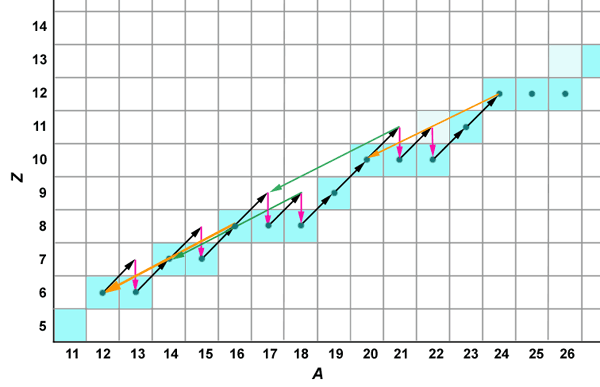
These reactions are not significant generators of energy, because
a) the seed nuclei are less abundant, and b) the higher nuclear charge
presents a higher coulomb barrier.