Outline
7D. Carbon and Oxygen Reactions
The main C and O reactions are (H&K)
| |
| Q
MeV | Channel
fraction |
| 12C + 12C | → |
20Ne + α |
4.621 | 44% |
| → |
23Na + p |
2.242 | 56% |
| 23Na + p | → |
20Ne + α |
2.379 |
| 23Na + p | → |
24Mg + γ |
11.691 |
| 16O + α | → |
20Ne + γ |
| 20Ne + α | → |
24Mg + γ |
| End result: | |
20Ne, 23Na, | 24Mg |
ε12C =
1.43×1042 ηQ ρ
X12C2
T9−3/2
e−84.165/T91/3
ergs g−1 s−1,
where ηQ is an appropriate fractional energy release per reaction.
12C + 16O reactions occur, but the rate is rather
slower than both C + C and at higher temperatures O + O. Besides, the carbon
is rapidly eliminated by the C + C reaction sequences.
| 16O + 16O | → |
28Si + α |
9.593 | 21% |
| → |
31P + p |
7.678 | 61% |
| → |
31S + n |
1.500 | 18% |
| 31S | → |
31P + e+ + ν |
| 31P + p | → |
28Si + α |
| 28Si + α | → |
32S + γ, etc. |
| End result: | |
28Si, 30Si, | 34S |
ε16O =
1.3×1052 ηQ ρ
X16O2
T9−2/3
e−[139.53/T91/3
+corrections]
ergs g−1 s−1.
7E. Photodisintegration and Silicon burning to Iron Group Equilibrium
Further reactions eventually leading to iron group equilibrium occur
by photodisintegration / re-association reactions.
As T9 approaches and exceeds unity, photon energies
rise to the MeV range and are able to spalate (chip off) p and α
particles from lower-mass nuclei (lower binding energy per nucleon),
which then combine with higher-mass nuclei (higher binding energy per
nucleon).
Examples:
1. 20Ne (γ,α) 16O, followed by
20Ne (α,γ) 24Mg (α,γ) 28Si
2. 28Si (γ,α) 24Mg
(α,p) 27Al (α,p) 30Si
The former happens at temperatures intermediate between carbon burning
and oxygen burning, and converts all Ne to O and Si.
Homework:
Show that converting two 20Ne into one 16O + one 24Mg
is exothermic, and three 20Ne into two 16O + one 28Si
is even more exothermic.
Below is figure 2.26 from H&K:
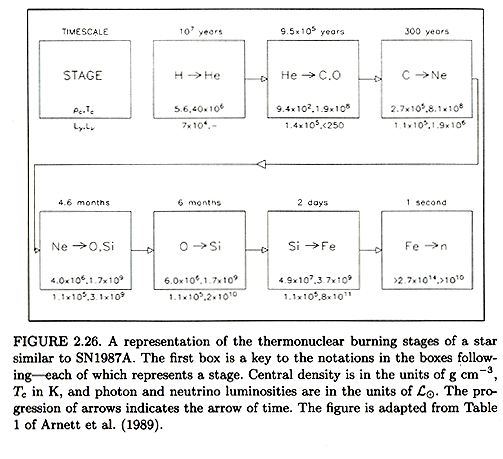
The nuclear statistical equilibrium (often refered to by the acronym NSE in
the literature) of the iron group depends on the time
available to achieve equilibrium.
The group elements start out predominantly as α-nuclei; i.e.
equal (and even) numbers of protons and neutrons.
These nuclei rapidly shuttle α's back and forth via photodisintegration
reactions.
The NSE may be calculated with the usual nuclear Saha equations,
and favors 56Ni.
But, 56Ni is proton-rich and beta decays with a half-life
of 6.077 days to 56Co, which in turn decays with a half-life
of 77.27 days to 56Fe.
If weeks are available for these and other beta decays to happen,
the equilibrium eventually favors 56Fe.
The table above suggests that weeks are not available.
In fact 56Co often appears in the spectra of supernovae,
indicating its very recent origin from 56Ni.
