The values of the eigenfrequencies are:
ω02 = 4.001 GM/R3
ω12 = 13.34 GM/R3
ω22 = 26.58 GM/R3
If we assume that oscillations do not exchange or block energy, we will gain a simple understanding of the oscillation modes and frequencies. We will lose ibformation about driving and damping mechanisms. Without energy exchange, we need only deal with the structure equations leading to the polytrope discussion:
4πr 2ρdr = dm
r 2r″dm = − 4πr 4dP −Gm dm
Equation of State:
P = Po
(ρ /ρo) β
(T /To) α
Here r″ is the local acceleration.
Now write the variables as:
y(m) [1 + δy(m, t) /y(m)],
where y(m) is the solution of the static equilibrium model.
Substitute into the equations preserving terms only linear in the perturbation:
4πr 2
(1 + 2 δr /r)
ρ
(1 + δρ /ρ)
[(1 + δr /r) dr + r d(δr /r)]
= dm
r 3 (1 + 2 δr /r) (δr /r)″ dm
+ 4πr 4 (1 + 4 δr /r)
[(1 + δP /P) dP + P d(δP /P)]
= Gm dm
Now subtract out the equilibrium solution from both equations (note− replace the dm factor in the acceleration term with the static 4πr 2ρdr from the continuity equation, and δρ /ρ with Γ1−1 δP /P):
3 δr /r
+ Γ1−1 δP /P
+ r d(δr /r) /dr
= 0
ρr (δr /r)″ dr
+ (4 δr /r
+ δP /P) dP
+ P d(δP /P)
= 0
Now, assume we are dealing with oscillating perturbations, and decompose into Fourier components:
δr /r = ζ(r) eiωt.
Substitute into the two eqiations above and rearange terms a bit:
dζ /dr = − (3ζ
+ Γ1−1 δP /P)
/r
d(δP /P) /dr =
− (dP /Pdr) (4ζ
+ ω2r 3ζ /Gm
+ δP /P).
Differentiate the first equation and eliminate δP /P by combining the two equations to get the linear adiabatic wave equation:
L(ζ ) ≡ − (1/ρr 4) d (Γ1 Pr 4dζ /dr) /dr − (ζ /ρr) {d [(3Γ1 − 4)P] /dr} = ω2ζ.
To solve the equation we need two boundary equations, related to the central condition on r and the surface condition on P in the structural equations:
The first of the two 1st-order equations is bounded the center:
3ζ
+ Γ1−1 δP /P = 0 at r = 0.
The second equation is bounded at the surface:
4ζ
+ ω2r 3ζ /Gm
+ δP /P = 0 at r = R.
Neither of these conditions ties the scale of ζ (e.g.
the amplitude of the oscillation) since the wave equation is homogeneous.
If we arbitrarily scale ζ = 1 at r = R, then we overdetermine
the 2nd-order differential equation, until we realize that ω is
a free variable.
A standard quantum-mechanics (or for that matter, organ pipe) problem.
Solutions ω2 = ωn2 are
eigenvalues and the corresponding ζ (r, ωn)
are eigenfunctions for those solutions.
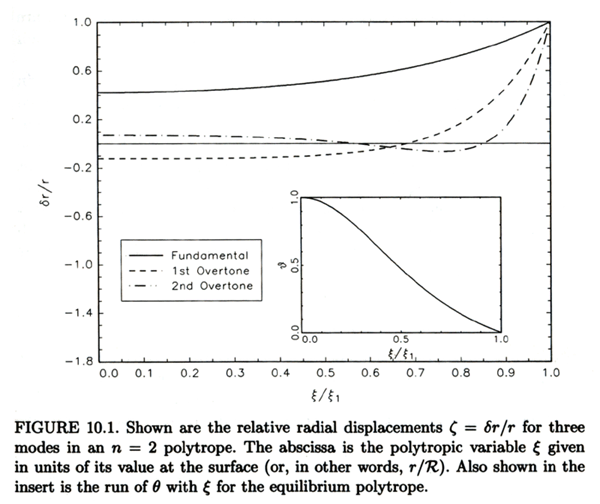
Below are the eigenfunction solutions for the first three radial modes in an
n = 2 polytrope as copied from H&K:

The values of the eigenfrequencies are:
ω02 = 4.001 GM/R3
ω12 = 13.34 GM/R3
ω22 = 26.58 GM/R3