1. Ans: 45 N. The torque=force*radius must balance.

2. Ans: 0.67 m. The center of mass is at (200*0+100*2)/(200+100).

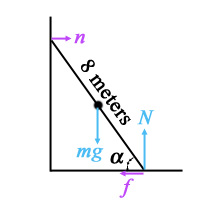
3. Ans: 51ø; a tricky one. If the wall were really rough, all angles would "hang on" and not slip, so "smooth" must be interpreted as frictionless. If the wall is frictionless, the only vertical forces on the ladder are mg and N, the normal force; these must balance. Therefore, N = −mg =100 N upward.
Now the torque about the top of the ladder must also =0 if there is no movement. if w =weight of ladder =mg =N, this torque is 4w*cos(a) +8*0.4N*sin(a) −8N*cos(a) =0, which becomes tan(a) =5/4.

4. Ans: 30 cm mark. As measured from the middle, we have −0.4*30+0.6*30+0.3*x =0 (to balance torques). The solution is −20 cm from the middle.

5. Ans: 850 N. The torque about the distant end of the platform must =0, so 3*800+2*500 = 4*T.

6. Ans: 69 N. The net torque about the pin =0, so T_vertical*6 =120*3, thus T_vertical =60 and T=60/sin(60ø).

7. Ans: 5.0 mm. Use formula DL= L₀(F/A)/g.

8. Ans: 2.0 x10⁸ N. Use formula DV= V₀(F/A)/B.