English translation of a 1799 essay by

Pierre Simon Laplace†

 

Proof of the theorem, that the attractive force of a heavenly body could be so large, that light could not flow out of it. ‡

 

(1) If v is the velocity, t  the time and s space which is uniformly moving during this time, then, as is well known, v  = s/t.

 

(2) If the motion is not uniform, to obtain the value of v at any instant one has to divide the elapsed space ds and this time interval dt into each other, namely v = ds/dt, since the velocity over an infinitely small interval is constant and thus the motion can be taken as uniform.

 

(3) A continuously working force still strive to change the velocity. This change of the velocity, namely dv, is therefore the most natural measure of the force. But as any force will produce double the effect in double the time, so we must divide the change in velocity dv by the time dt in which it is brought about by the force P, and one thus obtains a general expression for the force P, namely­

                                 

 

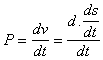
Now if dt is constant.

 

                                  

 

accordingly            

 

† Algemeine geographische Ephemeridien herausgegeben von F. von     Zach. IV Bd, 1 St., I Abhandl., Weimar 1799. We should like to thank D. W. Dewhirst for providing us with this reference. See also note at end of this Appendix.

‡ This theorem, that a luminous body in the universe of the same  density as the earth whose diameter is 250 times larger than that of the sun, can by its attractive power prevent its light rays from reaching us, and that consequently the Largest bodies in the universe could remain invisible to us, has been stated by Laplace in his Exposition du Système du Monde , Part II, p. 305, without proof. Hero is the proof. Cf. A.G.E. May 1798, p. 603. v. Z.

 

 

 

(4) Let the attractive force of a body = M; a second body, for example a particle of light, finds itself at distance r; the action of the force M on this light particle will be—M/rr; the negative sign occurs because the action of M is opposite to the motion of the light.

 

(5)   Now according to (3) this force also equals ddr/dt2, hence

 

                                   

 

Multiplying by dr,      

 

integrating,                 

 

where C is a constant quantity. or

                                

Now by (2) dr/dt is the velocity v, accordingly

 

                                 

holds, where v is the velocity of the light particle at the distance r.

 

(6) To now determine the constant C, let R be the radius of the attracting body, and a the velocity of the light at the distance R, hence on the surface of the attracting body; then one obtains from (5) a2 = 2C+2M/R , therefore 2C = a2 ‑ 2M/R. Substituting this in the previous equation gives

                

 

(7) Let R' be the radius of another attracting body, its attractive power be iM, and the velocity of the light at a distance r be v', then according to the equation in (6)

 

                           

(8) If one makes r infinitely large, the last term in the previous equation vanishes and one obtains

 

                          

The distance of the fixed stars is so large, that this assumption is justified.

 

(9) Let the attractive ponder of the second body be so large that light cannot escape from it; this can be expressed analytically in the following way: the velocity v' of the light is equal to zero. Putting this value of v' in the equation (8) for v', gives an equation from which the mass iM for which this occurs can be derived. One has therefore

                              or       

 

 (10) To determine a, let the first attracting body be the sun; then a is the velocity of the sun’s light on the surface of the sun.  The attractive power of the sun is however so small in comparison with the velocity of light, that one can take this velocity as uniform.  From the phenomena of aberration it appears that the earth travels at 20”in its path while the light travels from the sun to the earth, accordingly: let V be the average velocity of the earth in its orbit, then on has a : V = radius (expressed in seconds) : 20” =  1 :  tang. 20”.

 

(11) My assumption made in Expos. du Syst. du Monde. Part II,

p. 305, is R' = 250R. Now the mass changes as the volume of the attracting body multiplied by its density the volume, as the cube of the radius. accordingly the mass as the cube of the radius multiplied by the density. Let the density of the sun = 1; that of the second body = r ; then

 

           M : iM = 1 R3 : rR’3 = 1 R3 : r 2503 R3

 

 or           1 : i = 1 : r(250)3

 

 or                i = (250)3r

 

(12) One substitutes the values of I and R’ in the equation a2=2iM/R’, and thus obtains 

 

        

 

                  

 

( 13) To obtain r, one must still determine M.  The force M of the sun is equal at a distance D to M/D2.  Let  D be the average

 

distance of the earth, V the average velocity of the earth; then this force is also equal to V2/D (see Lande's Astronomy, III, §3539). Hence M/D2 = V2/D or M = V2D. Substituting this in the equation (12) for r gives

 

,

 

         according to (10)

 

   tan average apparent radius of O

 

from which r is approximately 4, or as large as the density of the earth.

 

D. W. Dewhirst adds:

 

The Allgemeine geographische Ephemerides was a journal founded by F. X. von Zach, of which 51 volumes were published between 1796 and 1816. The footnote (‡) is a translation of that added by von Zach to the original paper which is however not very helpful to the modern reader.

 

There are no less than 10 different editions of Laplace’s Exposition du Système du .Monde published between 1796 and 1835, some in one quarto volume and some in two volumes octavo. In the earlier editions the 'statement without proof' comes a few pages before the end of Book 5, Chapter 6, though Laplace removed the specific statement. from later editions.

 

The reference by von Zach to A.G.E. May 1798, p. 603, seems to be a mistake on von Zach's part: he was perhaps intending to refer to A.G.E. Vol. I, p. 89, 1798 where there is an extensive essay review of the first edition of Laplace's Exposition du Système du Monde.