This is homework assignment 13, due on Friday, 3rd December.
1. Do problem 5.26, 5.29 and the following problem. Special note: Following problem cancelled. You need not do it!
Solutions
2. A hoop of mass M is free to rotate in its own plane under the influence of gravity about a point P on its edge which is held fixed as shown in the figure. A bead of mass m, located at point B, is constrained to move only on the hoop. The point C is the center of the hoop. The angles a and b are measured with respect to the vertical lines passing through P and C.
![]()
![]()
![]()
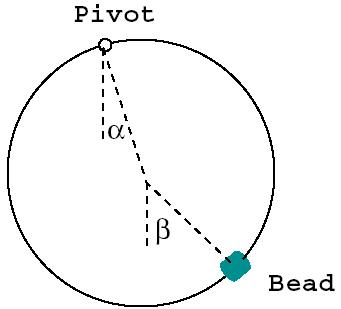
(a) Find the Lagrangian for the system in terms of the two angles.
(b) Approximate L so that the problem reduces to that of small oscillations.
(c) Find the eigenfrequencies and eigenvectors corresponding to the normal modes. You need not normalize the eigenvectors.