Island Nucleation and Growth

Island nucleation and growth during the early stages of epitaxial deposition on a high-symmetry surface play an important role in determining the later stages of growth. Both the submonolayer island density and morphology strongly influence the later stages of growth. Recent work has focused on the dependence of the island-density and size distribution on the critical island size.

Recently, Bales and Chrzan have developed a self-consistent rate-equation theory which accurately predicts the average island density as a function of coverage for a given critical island size. However - due to the neglect of correlations - such a mean-field theory does not accurately predict the island-size distribution.

In recent work, we have studied the dependence of the island-size distribution on the critical island size, and have also used rate-equation theory to study the crossover in the critical island size as a function of deposition rate and substrate temperature.

Current Research

With Mihail Popescu and Fereydoon Family of Emory University, we are developing an improved self-consistent rate-equation theory which explicitly takes into account the correlation between the island size s and the area of the depletion zone surrounding an island. The goal is to accurately predict the island-size distribution as a function of deposition parameters such as the deposition rate and/or substrate temperature.

We are currently applying this theory to the study of submonolayer epitaxy in both one- and two-dimensions. In the case of one-dimensional growth (corresponding to deposition at steps) fluctuations turn out to play an important role. We are also extending this work in order to study the dependence of the island-size distribution on deposition parameters for the case of higher critical island size and for the case of heteroepitaxial growth such as in InAs/GaAs quantum dots.

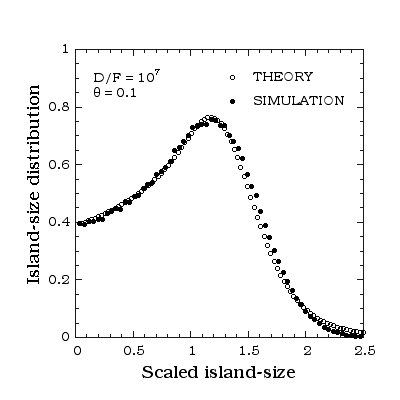
Scaled island-size distribution corresponding to deposition of 3D islands on a two-dimensional substrate with critical island size i = 1 at coverage 0.1 ML with D/F = 1.e7 where D = diffusion rate and F = deposition rate. Filled symbols are kinetic Monte Carlo results while open symbols are results from self-consistent rate-equation theory.